Théorème de Thalès fait parti des cours les plus importants au Brevet. En voyant les anciens examens, tu as toujours un exercice sur ce Théorème. Parfois, les exercices ou tu as des questions sur ce théorème, tu peut y avoir aussi des questions sur le Théorème de Pythagore.
Contenu
Théorème de Thalès ( Enoncé ) :
Ce Théorème est une propriété qui permet de calculer des longueurs dans certaines figures géométriques.
L’ application du Théorème de Thalès, nécessite d’avoir deux droites parallèles coupées par deux droites sécantes.
Dans les exercices qui traite le Théorème de Thalès, tu as une des deux configurations :
Théorème de Thalès : Configuration 1
Les deux droites parallèles se trouvent au même côté par rapport au point d’intersection ( le point A ) des deux droites sécantes.
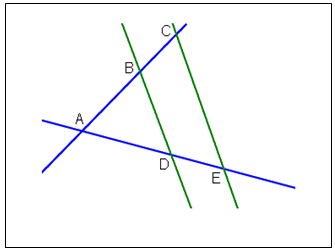
Énoncé du Théorème :
On a les points A,B,C et A,D,E sont alignés sur deux droites sécantes en A.
Si les deux droites (BD) et (CE) sont parallèles, alors :
![]()
Théorème de Thalès : Configuration 2
Le point d’intersection des deux droites sécantes ( le point B ) se trouve entre les deux droites parallèles :
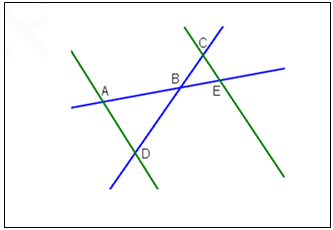
Énoncé du théorème :
On a les points A,B,E et D,B,C sont alignés sur deux droites sécantes en B.
Si les deux droites (AD) et (CE) sont parallèles, alors :
![]()
Exos d’application sur le théorème de Thalès :
Exercice 1 :
( Voir la correction dans la vidéo ci-dessous )
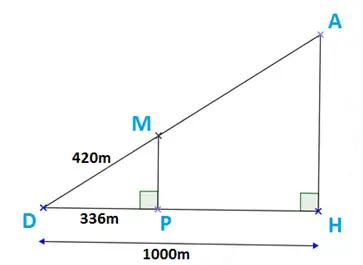
Un funiculaire part de D pour se rendre à A suivant la droite (DA).
DM = 420m ; DH = 1000m; DP = 336m
Les triangles DMP et DAH sont respectivement rectangles en P et H.
- Calculer la distance DA en mètre.
Solution :
Le triangle DMP est rectangle en P. Donc ( MP ) et ( DH ) sont perpendiculaires en P.
Le triangle DAH est rectangle en H. Donc ( AH ) et ( DH ) sont perpendiculaires en H.
Donc : ( MP) et (AH) sont parallèle.
Les deux droites (MA) et (PH) sont sécantes en D.
D’après le Théorème de Thalès, on a :

Exercice 2 :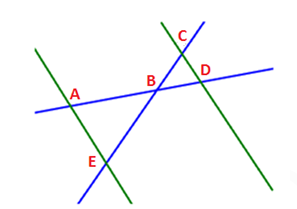
(AE) et (CD) sont parallèles
BA = 6 cm ; BE = 8,4 cm ; BD = 4 cm et CD = 3 cm.
Calculer BC puis AE.
Solution :
On sait que :
– Les points D,B,A sont alignés ainsi que les points C,B,E
– Les droites (CD) et (AE) sont parallèles.

5 d’autres Exercices Corrigés sur ce Théorème et sa Réciproque à Télécharger en pdf.
Autres liens utiles :
- Réciproque et Contraposée du Théorème de Thalès
- Produit en Croix
- Propriétés des Droites Parallèles et Perpendiculaires
- Théorème de Pythagore ( Introduction )
- Calcul de la longueur d’un côté dans un triangle rectangle
- Réciproque du Théorème de Pythagore ( Exercice d’ Application )
- Contraposée du Théorème de Pythagore
Si ce n’est pas encore clair pour toi sur le Théorème de Thalès, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête