Contenu
Introduction sur le Théorème de Pythagore :
Théorème de Pythagore fait parti des cours de géométrie au niveau 4ème et 3ème sans oublier sa grande importance à l’examen du Brevet des collèges. Ce théorème, met en relation les longueurs des côtés d’un triangle rectangle en permettant de calculer l’un des trois côtés en connaissant les deux autres côtés.
Angle Droit, Triangle Rectangle et Hypoténuse ?
C’est quoi un Angle Droit ?
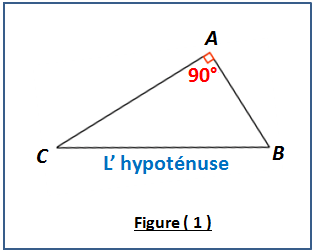
Un angle droit mesure 90°.
L’angle CAB dans le triangle ABC ( Figure 1 ).
C’est quoi un triangle rectangle ?
Un triangle rectangle est un triangle qui contient un angle droit ( le triangle ABC est rectangle en A ).
C’est quoi l’ Hypoténuse ?
L’ hypoténuse est le côté opposé à l’angle droit dans un triangle rectangle. Dans la figure 1, le côté BC est l’hypoténuse. En plus, l’hypoténuse, est toujours le plus long côté des trois côtés du triangle.
La vidéo ci-dessous, explique le Théorème de Pythagore avec un rappel sur la définition d’un angle droit, un triangle rectangle et l’ hypoténuse.
Théorème de Pythagore :
Énoncé du Théorème de Pythagore :
Si un triangle est rectangle, le carré de la longueur de son hypoténuse ( le côté opposé à son angle droit ) est égal à la somme des carrés des longueurs de ses deux autres côtés.
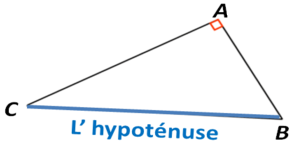
On prend l’ exemple du triangle rectangle ABC rectangle en A, on a donc cette égalité :
BC² = AB² + AC² ( Le carré de l’hypoténuse est égal à la somme du carrée des deux côtés de l’angle droit ).
Pour maîtriser ce Théorème, je t’invite à voir aussi l’application de ce théorème pour Calculer la longueur d’un côté dans un Triangle Rectangle. En plus, tu as la Réciproque et la Contraposée du théorème de Pythagore.
Exercices d’Application : Théorème de Pythagore
Exercice 1 :
Nous avons un triangle ABC rectangle et nous avons les longueurs suivantes : AC = 5 cm, BC = 3 cm et AB = 4 cm.
1/ devine l’ hypoténuse et le sommet ou le triangle ABC est rectangle ?
2/ écris l’égalité de Pythagore appliquée à ce triangle rectangle.
Corrigé :
1/
- On remarque que le côté le plus long est AC = 5cm. Donc, AC représente l’ hypoténuse du triangle.
- AC représente l’ hypoténuse, donc, le triangle ABC est rectangle en B.
2/
Vu que AC est l’hypoténuse, l’égalité de Pythagore est sous la forme :
AC² = AB² + BC²
( En remplaçant par les valeurs des longueurs : AC² = 5² = 25 et AB² + BC² = 3² + 4² = 9 + 16 = 25 )
Exercice 2 :
On considère la figure suivante :
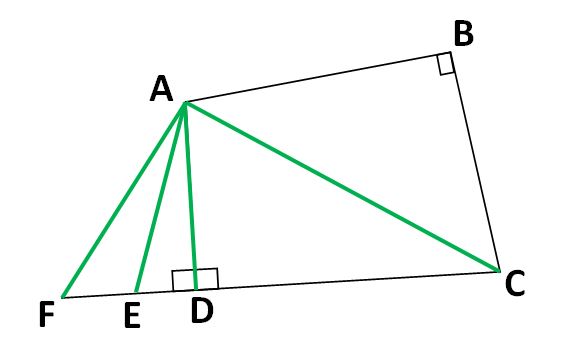
1/ Cite quatre triangle rectangle sur la figure ci-dessus.
2/ Applique le théorème de Pythagore aux triangles rectangles de la figure ci-dessus et Compléter les égalités suivantes :
AF² = … ?
AE² = … ?
AC² = … ?
AC² = … ? ( la deuxième réponse est différente de la première )
Corrigé :
1/ les quatre rectangles rectangles sont : ABC, ACD, ADE et ADF
2/
AF² = DF² + DA² ( le triangle utilisé est ADF rectangle en D )
AE² = DE² + DA² ( le triangle utilisé est ADE rectangle en D )
AC² = BA² + BC² ( le triangle utilisé est ABC rectangle en B )
AC² = DA² + DC² ( le triangle utilisé est ACD rectangle en D )
Autres liens utiles :
- Calculer une longueur dans un triangle rectangle
- Réciproque de Pythagore
- Contraposée de Pythagore
- Théorème de Thalès
- Réciproque et Contraposée du Théorème de Thalès
- Formules d’Aires et de Volumes
- Agrandissement ou réduction de rapport k ( k > 0 ou k < 0 )
Si ce n’est pas encore clair pour toi sur le Théorème de Pythagore , n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
