Ce cours sur les dérivées, tu as la définition de la dérivée d’une fonction, le tableau de fonctions dérivées usuelles dont on a besoin à connaître au niveau lycée dans l’étude de fonctions et tu as un quiz à faire à la fin de ce cours.
Contenu
Dérivée d’une Fonction:
Origine du mot dérivée :
L’origine du mot « dérivé » est le mot latin « derivare » qui signifiait « détourner un cours d’eau ». Le mathématicien franco-italien Joseph Louis Lagrange (1736 ; 1813) a introduit le mot « dérivé » pour signifier que la nouvelle fonction dérive d’une autre fonction (au sens de « provenir »).
Définition :
Le calcul de la dérivée est très importante dans l’étude de fonctions. Elle permet d’ étudier le signe et la variations de la fonction et il n’y a des formules à apprendre, et une fois que tu les connais, ça devient très simple !!
La dérivée d’une fonction f ( x ) en x = a (écrite sous la forme f ‘(a) et qu’ on prononce f prime de a) est le coefficient directeur de la tangente à la courbe au point d’ abscisse a.
Remarque : La dérivée d’ une fonction est UNIQUE : Si une fonction est dérivable sur un intervalle, elle n’admet qu’ une seule fonction dérivée.
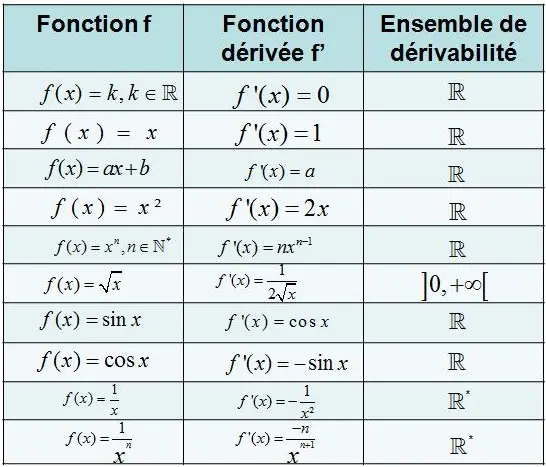
Tableau de Fonctions Dérivées Usuelles:
Cette partie du cours présente le tableau des fonctions dérivées usuelles à connaître au Lycée et tu as aussi quelques démonstrations du calcul de dérivée.
List de Fonctions Dérivées Usuelles:
Savoir comment calculer la dérivée f ‘ d’ une fonction f est très simple en apprenons les formules des drivées usuelles par coeur et ça sera très facile avec la pratique. Aussi, en connaissant les Opérations sur les Dérivées.
Voici une série de Fonctions Dérivées Usuelles à connaître:
Démonstration de quelques Dérivées Usuelles:
Démonstration Dérivée de la Fonction Carrée:
Le premier exemple de démonstration du calcul de la Dérivée d’un Polynôme : Fonction Carrée.
Soit la fonction f définie sur R par f ( x ) = x 2.
Calculons le nombre dérivé de la fonction f en un nombre réel quelconque a.
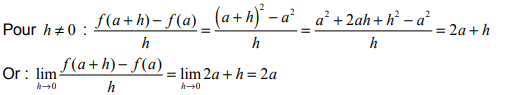
On associe, pour tout nombre a, le nombre dérivé de la fonction f égal à 2a. On a défini donc sur R une fonction, notée f ‘ ayant comme expression: f ‘(x) = 2x.
Cette fonction s’appelle la fonction dérivée de f.
( Voir exemples de calcul de dérivée des Polynômes )
Démonstration Dérivée de la Fonction Inverse:
Le deuxième exemple de démonstration du calcul de la dérivée est celui de la Fonction Inverse.
Soit la fonction f définie sur R\{0} par f (x) = 1/x .
Calculons le nombre dérivé de la fonction f en un nombre réel quelconque a.
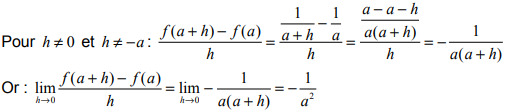
On associe, pour tout nombre a, le nombre dérivé de la fonction f égal à -1/a²
Ainsi, pour tout x de R\{0}, on a : f (x) = -1/x²
( Voir exemples de calcul de dérivée des Fonctions Rationnelles )
Quiz sur le Calcul des Dérivées:
Pour réussir le calcul des dérivées au Quiz, tu peux voir aussi ce cours: Opérations sur les Dérivées.
Ça sera mieux que tu essayes de calculer la dérivée tout seul et ensuite, tu choisis la bonne réponse:
Autres liens utiles sur les dérivées:
- Dérivée d’une Fonction contenant la Racine Carrée
- Opérations sur les Fonctions Dérivées
- Calculateur de Dérivée en Ligne – Calcul Fonction Dérivée
Si tu as des questions sur comment calculer la dérivée d’une fonction ou sur le tableau de fonctions dérivées usuelles, n’hésite surtout pas de laisser un commentaire en bas ou nous écrire sur notre Page Facebook.

