Résolution d’ équation du second degré dans ℂ

Nous allons voir dans ce cours la Résolution d’ équation du second degré dans ℂ qui représente l’ Ensemble des Nombres Complexes.

Résolution d’ équation du second degré dans ℂ

Définition :

Une équation de second degré d’inconnue z s’écrit sous la forme az²+ bz + c = 0  où a, b et c sont des nombres réelles avec a ≠ 0

Résoudre une équation d’inconnue z dans  l’ensemble des nombres complexes, c’est trouver les valeurs complexes z qui vérifient l’ égalité en question.

Rappel :

i est le nombre complexe ayant le carré qui vaut -1 :  i² = – 1

Quelques Puissances de i :

i² = – 1    ;    i³ = i² x i = – i    ;    i⁴ = i² x i² = 1    ;    i⁵ = i² x i² x  i = i  ; … etc.

Résoudre dans ℂ  une Équation du Second Degré :

Soit a, b et c des réels avec a ≠ 0.
On appelle discriminant du trinôme az² + bz + c , le nombre réel, noté Δ, égal à b² − 4ac.

– Si Δ > 0 : L’équation az² + bz + c = 0 a deux solutions réelles distinctes :

– Si Δ = 0 : L’équation az² + bz + c = 0 a une unique solution réelle : z₀ = − b/2a

– Si Δ < 0 : L’équation az² + bz + c = 0 a deux solutions complexes distinctes :

Exercices Corrigés ( Equation de degré 2 dans ℂ  ) :

Résoudre dans ℂ  une équation du second degré :

Exemple 1 :  z² + 7 = 0

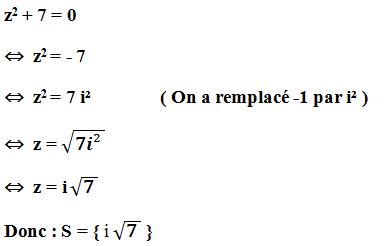
Exemple 2 :  z² + 4z + 5 = 0

Δ = b² – ac = 4² – 4*1*5 = 16 – 20 = – 4

Δ < 0 donc l’équation admet deux solutions complexes conjugués :

Δ = – 4 = 4 i² 

---

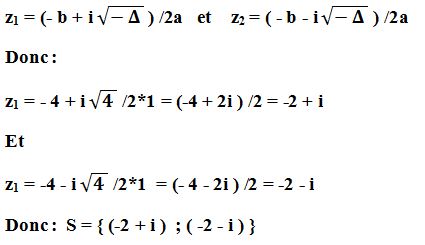
Autres Liens sur les Nombres Complexes

• Nombres Complexes ( Ensemble ℂ, Forme Algébrique, Inverse, Conjugué & Module )
• Pour les curieux sur l’ Histoire des Nombres Complexes

---