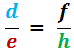Contenu
Produit en Croix ou Règle de 3 :
Dans un tableau de proportionnalité, le Produit en Croix, nous permet à partir de 3 valeurs connues, de déterminer la quatrième valeur pour qu’il y ait proportionnalité. On dit que l’on calcule » la quatrième proportionnelle « .
Le Produit en Croix est aussi appelé la Règle de 3 et elle est souvent utilisée pour calculer une longueur en utilisant le Théorème de Thalès.

Supposant qu’on a l’égalité suivante :
![]()
Suivant ce qu’on cherche à calculer ( a, b, c ou d ) , l’expression change :
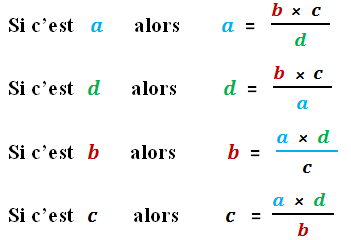
Produit en Croix : Exercices Corrigés
Application du Produit en Croix : Cas d’ égalité de deux quotients
Exemple 1 :
Supposant qu’on a l’égalité suivante :
tel que b = 7, c = 20 et d = 28 et on cherche à calculer a ?
Suivant la méthode du Produit en Croix :
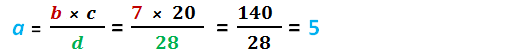
Donc, a = 5
Exemple 2 :
Supposant qu’on a l’égalité suivante :
tel que d = 2 , e = 9 et f = 14 et on cherche à calculer h ?
Suivant la méthode du Produit en Croix : 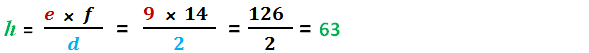
Donc, h = 63
Calcul de la Quatrième Proportionnelle :
Pour acheter 5 kilos de pommes, nous avons payé 34,5 euros.
Question : Combien faut-il payer pour acheter 2 kilos de pommes ?
Solution : Soit x le prix de 2 kilos de pommes.
On peut mettre les valeurs dans un tableau :
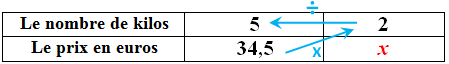
Donc, en appliquant la Règle de 3 :
![]()
Le prix de 2 kilos de pommes est 13,8 euros.
Application de la Règle de Trois : Question du Brevet 2015
On prend l’exemple de l’exercice 5 Question 1 Brevet 2015 ( Sujet et Correction du Brevet Math 2015 ) :
Un pot de peinture permet de peindre une surface de 24m². On a calculé l’Aire Total de la surface à peindre qui est égal à 56,25 m².
Question : Combien de pots faut-il pour peindre la façade d’une surface de 56,25 m² ?
Solution : Soit x le nombre de pots qu’il faut pour peindre une surface de 56,25m²
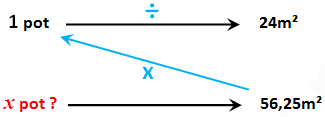
En appliquant le Produit en Croix :
![]() Donc, il nous faut 3 pots.
Donc, il nous faut 3 pots.
Application de la Règle de Trois : Cas du Théorème de Thalès
On prend l’exemple de l’exercice 3 question 2 du Brevet Math 2015 du métropole ( Sujet et Correction du Brevet Math 2015 ) :
On applique le Théorème de Thalès :
![]()
Puis on remplace par les valeurs :
![]()
On calcule AP :
PD + AP = AD
⇔ AP = AD – PD
⇔ AP = 60 – 45
Donc : AP = 15
On remplace AP par sa valeur et on applique le Produit en Croix :

Donc, HP = 2,75 cm
Autres liens utiles : Théorème de Thalès et Pythagore :
- Introduction sur le Théorème de Pythagore
- Calculer une longueur dans un triangle rectangle
- Réciproque du théorème de Pythagore
- Contraposée du Théorème de Pythagore
Si ce n’est pas encore clair pour toi sur le Produit en Croix ( ou Règle de 3 ) , n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête