Ce cours de math présente la définition de la primitive d’ une fonction, des exemples simples à comprendre et le tableau de primitives de fonctions usuelles.
Si une fonction est dérivable sur un intervalle, elle n’admet qu’ une seule fonction dérivée. Par contre, une fonction qui admet une primitive, elle en admet automatiquement une infinité. Donc, on peut très bien dire que l’ on calcule « la » dérivée et que l’on recherche « une » primitive.
Contenu
Définition : Primitive d’une Fonction
Prenons f une fonction définie et dérivable sur un intervalle I.
f admet une primitive F sur l’ intervalle I Si F est dérivable sur I et : F'( x ) = f ( x )
Calcul de la dérivée et Calcul de la Primitive sont deux démarches inverses et pour vérifier qu’une fonction F est une primitive d’une fonction f, il suffit juste de vérifier que f est la dérivée de F.
Exemple 1 :
f(x) = 2x , alors F(x) = x2 est la primitive de 2x, puisque ( x2 )’ = 2x.
Exemple 2 :
f(x) = 4x – 1 , alors F(x) = 2x 2 – x est la primitive de 4x – 1, puisque ( 2x 2 – x )‘ = 4x – 1
Exemple 3 :
f(x) = cos (x) , alors F(x) = sin (x) est la primitive de cos (x) , puisque ( sin(x) ) ‘ = cos (x)
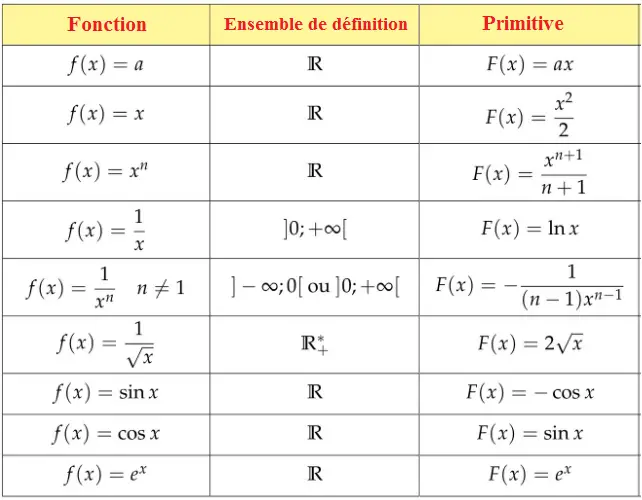
Tableau de Primitives de Fonctions Usuelles
Le tableau ci-dessous, présente plusieurs fonctions usuelles, leurs ensemble de définition et primitives.
Remarque :
Puisque la dérivée d’une fonction constante est nulle, si f admet une primitive sur un intervalle I, alors elle en admet une infinité sur cet intervalle. L’ensemble des primitives de f est donc donné à une constante près.
Autres liens utiles sur les fonctions :
Calculateur de dérivée en ligne, Opérations sur les dérivées, Calcul dérivée d’un Polynôme , Dérivée d’une Fonction Rationnelle , Dérivée d’une fonction contenant la Racine Carrée, Tableau de formules de dérivées usuelles
Si ce n’est pas encore clair sur le Tableau des Primitives de Fonctions Usuelles, n’hésite surtout pas de nous écrire sur notre Instagram ou nous laisser un commentaire.
En tout cas, Bravo d’avoir lu ce cours jusqu’au bout et tu peux le partager avec tes amis pour qu’eux aussi puissent en profiter 😉 !
