Pour effectuer L’ addition de fractions et la soustraction, on doit avoir des dénominateurs égaux. Par contre, la multiplication de fractions , ce n’est pas nécessaire d’ avoir ou de réduire les fractions au même dénominateur.
Méthode de multiplication de fractions :
Dans le cas de multiplication de fractions , le résultat est une fraction dont le numérateur est le produit des numérateurs des fractions et le dénominateur est égal au produit des dénominateurs :
Prenons 4 nombres a, b, c et d ( en sachant que b et d doivent être différent de 0 ) :
![]()
Remarque :
Le dénominateur d’une fractions doit toujours être différent de 0.
Solution de l’exercice ( voir la vidéo ci-dessus )
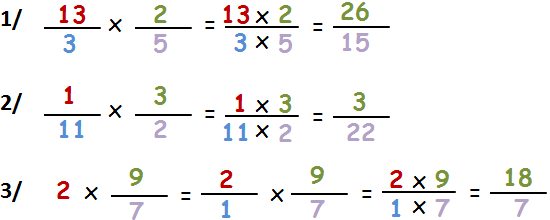
Dans les 3 exemples, les fractions sont simplifiées au maximum. Si ce n’est pas le cas, il faut simplifier.
(C’est plus facile de le faire avant d’effectuer la multiplication !)
Autres Exemples corrigés :
Exemple 1 :
(4 / 3) x (11 / 7)
= (4 x 11) / (3 x 7)
= 44 / 21
Exemple 2 :
(12 / 11) x (2 / 4)
= (12 / 11) x (1 / 2) ( On a simplifié la fraction 2 / 4 par 2 : 2 / 4 = (2 x 1 / 2 x 2 ) = 1 / 2 )
= (12 x 1) / (11 x 2)
= (6 x 2) / (11 x 2) ( 12 x 1 = 12 = 6 x 2 et On a simplifié la fraction par 2 )
= 6 / 11
Exemple 3 :
(5 / 2) x (6 / 25)
= (5 x 6) / (2 x 25)
= (5 x 2 x 3 ) / (2 x 5 x 5 )
= 3 / 5
Dans cette exemple, à la deuxième ligne, on a décomposer 6 = 2 x 3 et 25 = 5 x 5 et on a simplifier la fraction par 5 x 2.
Remarque :
Tout nombre peut être écrit sous forme d’une fraction avec un dénominateur égal à 1 ( C’est ce qui a été appliqué dans le 3ème exemple ).
Autres liens utiles :
Si ce n’est pas encore clair pour toi sur la multiplication de fractions , n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
