Nous allons voir comment trouver l’ inverse d’ un nombre relatif non nul et celui d’une fraction ( à condition que le numérateur et le dénominateur soient non nul ).
Contenu
Inverse d’ un nombre :
L’ inverse d’ un nombre relatif a non Nul est : 1/a
Le produit de deux nombres qui sont des inverses est toujours égal à 1 :
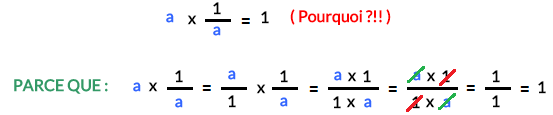
Exemples Inverse d’un Nombre :
⇒ Inverse de 6 est 1/6
⇒ Inverse de 21 est 1/21
⇒ Inverse de -3 est 1/-3
⇒ Inverse de 4 est 1/4 ( ou 0,25 puisque 1/4 = 0,25 )
⇒ Inverse -8 est 1/-8 ( ou -0,125 puisque 1/-8 = -0,125 )
Remarque :
Le produit de 0 par n’importe quel nombre est toujours égal à 0 : 0 x n’importe quel nombre = 0 Donc, 0 n’a pas d’inverse.
Inverse d’ une fraction :
Soit a et b deux nombres relatifs ( a et b est non Nul ).
Inverse de a/b est b/a
Et on dit que a/b et b/a sont des inverses et leur produit est égal à 1 :
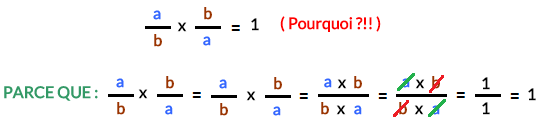 Exemples d’ Inverse d’ une Fraction :
Exemples d’ Inverse d’ une Fraction :
Inverse de 5/9 est 9/5 parce que leur produit est égal à 1 : 5/9 x 9/5 = 5x9 / 9x5 = 45/45 = 1
Inverse –2/3 et 3/-2 parce que leur produit est égal à 1 : -2/3 x 3/-2 = (-2)x3 / 3x(-2) = -6/-6 = 1
Autres liens utiles :
- Produit d’un nombre et d’un quotient
- Comment effectuer l’addition de nombres relatifs ?
- Multiplication de nombres relatifs
- Quotient : Définition et Signe
Si ce n’est pas encore clair pour toi sur l’ Inverse d’ un nombre et d’ une Fraction , n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
