Dans ce cours sur l’encadrement et les opérations, nous allons voir un rappel sur la représentation graphique d’ une inégalité, Comment représenter graphiquement un encadrement et calculer son Amplitude ainsi que l’ ordre et les opérations.
Contenu
Amplitude d’un encadrement ?
Si x > a et x < b on écrit : a < x < b ( x strictement supérieur à a et strictement inférieur à b )
Cette écriture est appelé un » encadrement « de x.
L’amplitude de cet encadrement est la longueur du segment qui a pour extrémités les points d’abscisses b et a soit b – a.
Encadrement et le Calcul de l’ amplitude :
Exemple 1 : Représentation graphique de l’encadrement
Définir un encadrement pour x tel que : x > 0 et x < 3
On a : x > 0 et x < 3 ( x est supérieur strictement à 0 et en même temps strictement inférieur à 2 )
Donc : 0 < x < 3
- La représentation graphique de x > 0 :
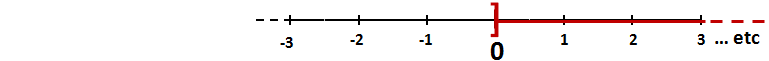
- La représentation graphique de x < 3 :
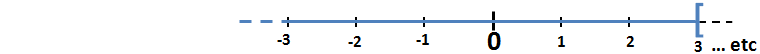
- La représentation graphique de l’encadrement 0 < x < 3 :
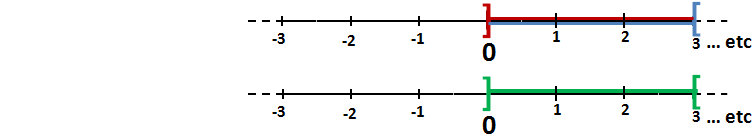
La représentation graphique de l’encadrement de x est la partie Verte ( L’ intersection des deux intervalles Marron et Bleu ) .
Donc, x peut prendre toutes les valeurs entre 0 et 3.
La valeur de x, ne peut ni être égal à 0 ni à 3 car les deux crochets sont ouverts vers l’extérieur de l’intervalle.
- L’amplitude de l’encadrement est 3 Car 3 – 0 = 3
Exemple 2 : Représentation graphique de l’encadrement
Définir un encadrement pour x tel que : x > -1 et x ≤ 1,5 :
On a : x > -1 et x ≤ 1,5
Donc, -1 < x ≤ 1,5
- La représentation graphique de x > -1 :

- La représentation graphique de x ≤ 1,5 :
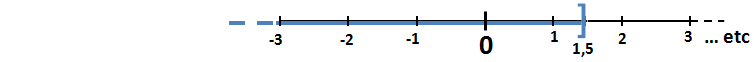
- La représentation graphique de l’encadrement -1 < x ≤ 1,5 :
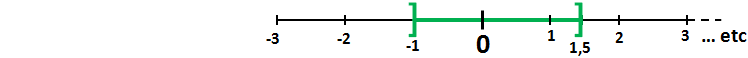
Donc, x peut prendre toute les valeurs entre -1 et 1,5 ( -1 exclus et 1,5 inclus ).
- L’amplitude de l’encadrement est 2,5 Car 1,5 – (-1) = 1,5 + 1 = 2,5
Ordre et Opérations :
Propriété 1 :
|
Prenons a, b et c des nombres relatifs : Si a < b Alors a + c < b + c Si a < b Alors a – c < b – c |
Exemple 1 : Sachant que a < -3,5 déduis-en une inégalité pour a + 7
Réponse :
On a : a < -3,5
Alors a + 7 < -3,5 + 7
Donc : a + 7 < 3,5
Exemple 2 : Sachant que a > 5 déduis-en une inégalité pour a – 7
Réponse :
On a : a > 5
Alors a – 7 > 5 – 7 Voir Comment additionner des nombres relatifs ?
Donc : a – 7 > -2
Propriété 2 :
|
Prenons a, b et c des nombres relatifs : Si a < x < b Alors a + c < x + c < b + c Si a < x < b Alors a – c < x – c < b – c |
Exemple 1 : Sachant que -2 < x < -1 déduis-en un encadrement pour x + 4
Réponse :
On a : -2 < x < -1
Alors -2 + 4 < x + 4 < -1 + 4
Donc : 2 < x + 4 < 3
Exemple 2 : Sachant que -2 < x < -1 déduis-en une inégalité pour x – 2
Réponse :
On a : -2 < x < -1
Alors -2 – 2 < x – 2 < -1 – 2
Donc : – 4 < x – 2 < -3
Propriété 3 :
|
Prenons a et b des nombres relatifs : Pour tout nombre c Positif : Si a < b Alors ac < bc Si a < x < b Alors ac < xc < bc Pour tout nombre c Négatif : Si a < b Alors ac > bc |
Remarque : Si a < b Alors -a > -b ( dans ce cas c = -1 donc, on inverse le sens du symbole de comparaison )
Exemple 1 : Sachant que x < -3,5 déduis-en une inégalité pour 7x
Réponse :
On a : x < -3,5
Alors 7 x x < 7 x ( -3,5 )
Donc : 7x < – 24,5
Exemple 2 : Sachant que 0 < x < -3 déduis-en un encadrement pour 9x.
Réponse :
On a : 0 < x < -3
Alors 9 x 0 < 9 x x < 9 x (-3)
donc : 0 < 9x < -27
Exemple 3 : Sachant que x < -2 déduis-en une inégalité pour -7x
Réponse :
On a : x < -2
Alors (-7) x x > (-7) x ( -2 )
Donc : -7x < 14
Exemple 4 : Sachant que x < -4 déduis-en une inégalité pour – x
Réponse :
On a : x < -4
Alors (-1) x x > (-1) x ( -4 )
Donc : –x < 4
Exemple 5 : Sachant que x > -3 déduis-en une inégalité pour -7x – 3
Réponse :
x > -3
⟺ (-7) x x < (-7) x ( -3 )
⟺ -7x < 21
⟺ -7x – 3 < 21 – 3
⟺ -7x – 3 < 18
Exemple 6 : Sachant que 0 < x < -5 déduis-en un encadrement pour 9x + 2
Réponse :
0 < x < -5
⟺ 9 x 0 < 9 x x < 9 x (-5)
⟺ 0 < 9x < -45
⟺ 0 + 2 < 9x + 2 < -45 + 2
⟺ 2 < 9x + 2 < -43
Propriété 4 :
|
Prenons a et b des nombres relatifs : Pour tout nombre c strictement positif ( c > 0 ) : Si a < b Alors a/c < b/c Pour tout nombre c strictement Négatif ( c < 0 ) : Si a < b Alors a/c > b/c |
Exemple 1 : Sachant que x < -6 déduis-en une inégalité pour x/3
Réponse :
x < -6
⟺ 1/3 x x < 1/3 x (-6)
⟺ x/3 < -6/3
⟺ x/3 < -2
Exemple 2 : Sachant que x > 2 déduis-en une inégalité pour –x/4
Réponse :
On a : x > 2
⟺ (-1/4) x x < (-1/4 ) x 2
⟺ –x/4 < -2/4
⟺ –x/4 < -1/2
Exo à faire : Encadrement et Représentation Graphique :
1/ Représenter graphiquement l’ inégalité suivante : x < -6 .
2/ Représenter graphiquement l’ encadrement suivant : 0 < x < -5 .
3/ Représenter graphiquement l’ encadrement suivant : 0 ≤ y < 8 .
4/ Représenter graphiquement l’ encadrement suivant : -4 < a ≤ 0 .
Déduit un encadrement pour : a + 1
5/ Représenter graphiquement l’ encadrement suivant : -2 ≤ y ≤ 1 .
Déduit un encadrement pour : –y + 2
6/ Sachant que x > 2 déduis-en une inégalité pour 2x
7/ Sachant que y < 5 déduis-en une inégalité pour y + 3
8/ Sachant que b < -2 déduis-en une inégalité pour –b/5
Autres liens utiles :
- Comment Représenter graphiquement une inégalité ?
- Comparaison de deux nombres relatifs
- Addition de Nombres Relatifs
Si ce n’est pas encore clair pour toi ou tu as des questions sur l’ Encadrement et Représentation Graphique d’ une inégalité ou d’ un encadrement, Ordre et les Opérations , n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
