Comment développer l’expression (a+b)(c+d) | Double Distributivité

Introduction sur la Double Distributivité : 

On applique la Double Distributivité pour développer ce type d’ expression : ( a + b ) ( c + d ) tel que a, b, cet dsont des nombres relatifs. 

Cette technique consiste à faire distribuer asur c et det on fait la même chose de bdistribué sur c et d (on applique la Simple Distributivité deux fois).

Quand on développe une expression en utilisant la simple ou la double distributivité, on a comme résultat une expression sans parenthèse. Contrairement à la Factorisation, on insère les parenthèses.

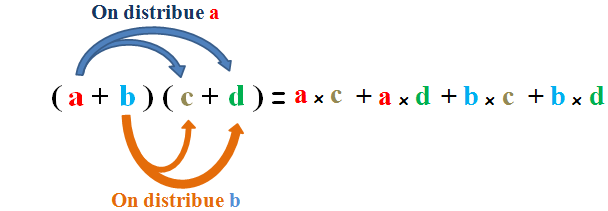
Double Distributivité expliquée en Vidéo :

Exemple 1 : ( x+ 2 ) ( x – 3 )

( x + 2 ) ( x – 3 ) = x x x  +  x  x (-3) + 2  x x + 2 x (-3) 

                                 =  x ² – 3x + 2x – 6

                                 =  x ² – x – 6

Exemple 2 : ( 2 –x ) ( x– 5 )

( 2 – x ) ( x – 5 ) = 2 x x + 2 x (-5) + (- x)  x x  + (- x)  x (-5) 

                               = 2x –  10  –  x ² +  5x

                               = – x ² + 7x –  10

Remarque : Il faut faire attention aux signes quand :

• tu fais la multiplication ( Rappel sur la multiplication des nombres relatifs )
• tu additionnes les nombres relatifs ( Rappel sur l’addition de nombres relatifs ) 

Exos à faire sur la Double Distributivité :

Exemple 1 :  A = ( x – 5 ) ( x + 10 ) 

Corrigé ( Voir la vidéo ) :

A = ( x – 5 ) ( x + 10 ) 

A =  x x x + x x 10 – 5 x x  – 5 x 10  

A =  x² + 10x – 5x  – 50  

A =  x² + 5x – 50  

 

Essaye de développer les expressions suivantes en utilisant la double distributivité et tu peux laisser tes réponses en bas en commentaire : 

Exemple 2 : B = ( 9 – x ) ( x – 2 ) 

Exemple 3 : C = ( x – 3 )( 7x + 5 ) – 10x

Exemple 4 : D = 11 – ( x + 5 )( 4x – 10 )

Exemple 5 : E = 13 + 7y – ( 6y – 10 )( 5 + 2y )  

---

Voir d’autres liens utiles :

• Comment développer une expression littérale (Simple Distributivité)?
• Comment factoriser une expression?
• Suppression des parenthèses dans une expression Littérale

• Addition de Nombres Relatifs
• Multiplication de Nombres Relatifs

---

Si ce n’est pas encore clair pour toi ou tu as des questions sur Comment développer une expression littérale de type ( a + b ) ( c + d ) en utilisant la Double Distributivité, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête