Savoir Comment Décomposer un Nombre en Produit de Facteurs Premiers est important comme il est demandé, à titre d’ exemple, à l’exercice 2 du Brevet de Math 2021.
Contenu
C’est quoi un nombre premier?
C’est quoi un Produit de Facteurs Premiers?
Un produit de Facteurs Premiers est un produit qui est sous la forme d’une multiplication de nombres premiers.
Exemple 1: 2 x 3 x 5
Exemple 2: 5 x 11 x 13
Exemple 3: 2 x 7 x 11 x 19
Décomposer un nombre en Produit de Facteurs Premiers:
Premièrement, on trace une droite verticale pour avoir 2 colonnes et on écrit le nombre à décomposer en haut de la colonne de gauche. Ensuite, la technique de la décomposition en produit de facteurs premiers consiste à diviser autant de fois que possible le nombre à décomposer par 2, puis par 3, par 5, par 7, par 11, par 13 …en suivant la liste des nombres premiers dans l’ordre croissant qu’on écrit à la colonne de droite. Puis, on refait la même chose aux nombres de la colonne gauche jusqu’à ce qu’on trouve 1 sur notre série de nombre de la colonne de gauche et on a la réponse qui est le produit de tous les nombres récupérés à la colonne de droite.
En général, dans la décomposition, si on obtient plusieurs facteurs identiques, on les élève à la puissance correspondante.
Exemple 1: 24
Décomposer 24 en produit de facteurs premiers
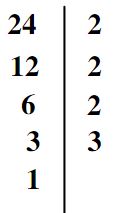
Donc: 24 = 2 x 2 x 2 x 3 = 23 x 3
Explication des étapes suivies:
La liste des nombres premiers est à garder toujours en tête ( 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, … )
1/ Le nombre à décomposer 24 est écrit en haut de la colonne de gauche.
2/ 24 peut être divisé par 2 : 24 / 2 = 12 ( on écrit 2 à la colonne de droit et 12 en bas de 24 à la colonne de gauche )
3/ 12 est divisible par 2 : 12 / 2 = 6 ( on écrit 2 à la colonne de droit et 6 en bas de 12 à la colonne de gauche )
4/ 6 est divisible par 2 : 6 / 2 = 3 ( on écrit 2 à la colonne de droit et 6 en bas de 3 à la colonne de gauche )
5/ 3 n’est pas divisible par 2 et divisible par 3 : 3 / 3 = 1 ( on écrit 3 à la colonne de droit et 1 en bas de 3 à la colonne de gauche )
On arrête puisqu’ on a trouvé 1. Donc 24 est égal au produit de tous les nombres de la colonne de droite:
24 = 2 x 2 x 2 x 3 = 23 x 3
Exemple 2: 33
Décomposer 33 en produit de facteurs premiers
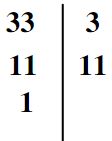
Donc: 33 = 3 x 11
Explication des étapes suivies:
1/ Le nombre à décomposer est 33.
2/ 33 n’est pas divisible par 2 et il est divisible par 3 : 33 / 3 = 11 ( on écrit 3 à la colonne de droit et 11 en bas de 24 à la colonne de gauche )
3/ 11 n’est pas divisible par 2, 3, 5, 7 et il est divisible par lui même 11 : 11 / 11 = 1 ( on écrit 11 à la colonne de droit et 1 en bas de 11 à la colonne de gauche )
On arrête puisqu’ on a trouvé 1.
Donc: 33 = 3 x 11
Exemple 3: 100
Décomposer 100 en produit de facteurs premiers
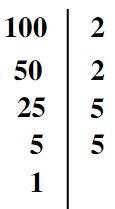
Donc: 100 = 2 x 2 x 5 x 5 = 22 x 52
Exemple 4: 156
Décomposer 156 en produit de facteurs premiers

Donc: 156 = 2 x 2 x 3 x 13 = 22 x 3 x 13
Exemple 5: 300
Décomposer 300 en produit de facteurs premiers
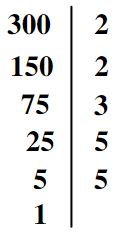
Donc: 300 = 2 x 2 x 3 x 5 x 5 = 22 x 3 x 52
Exercice à faire:
Décompose en produit de facteurs premiers les nombres suivants:
- 132
- 198
- 240
- 294
- 385
Si la technique de la décomposition n’est pas encore clair, n’ hésite pas de nous écrire en bas en commentaire ou via instagram.
