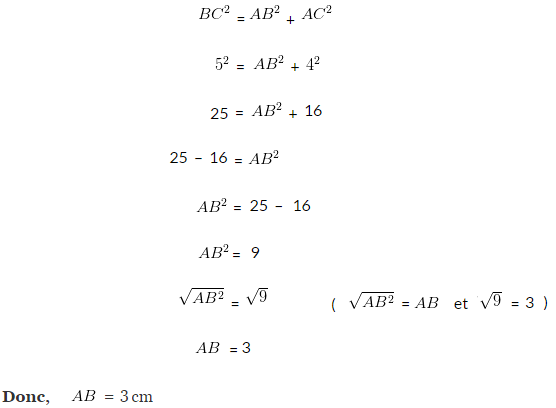Nous allons voir dans ce cours, comment calculer une longueur dans un triangle rectangle ( Hypoténuse ou l’ un des deux autres côtés de l’ angle droit).
Contenu
Calculer une longueur dans un triangle rectangle
On peut calculer une longueur dans un triangle rectangle en appliquant le fameux Théorème de Pythagore : En connaissant la longueur de deux côtés du triangle rectangle, on peut calculer la longueur du troisième côté.
Prenons le cas d’un triangle ABC, rectangle en A :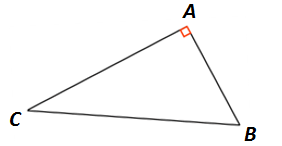
Donc, d’après la Formule de Pythagore, on a : BC² = AB² + AC²
La vidéo ci-dessous, explique à l’aide de 3 exercices, comment appliquer la Formule de Pythagore pour calculer une longueur dans un triangle rectangle ( la longueur de l’hypoténuse ou celle de l’un des deux côtés de l’angle droit ).
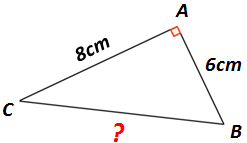
Exercice 1 : Calcul de la longueur de l’ Hypoténuse.
ABC est un triangle rectangle en A ( AC = 8cm, AB = 6cm et BC = ? ).
Question : Calculer la longueur du côté BC.
Solution :
Le triangle est rectangle en A, donc l’ hypoténuse est le côté BC ( le côté opposé à l’angle droit ) .
Donc, on applique le Théorème de Pythagore :
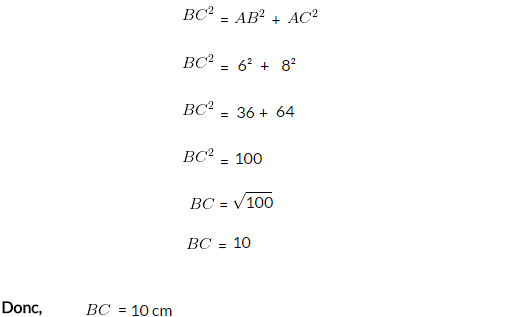
Exercice 2 : Calcul de la longueur de l’un des 2 côtés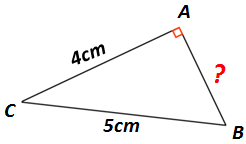
Le triangle est rectangle en A ( AC = 4cm, BC = 5cm et AB = ? ).
Question : Calculer la longueur du côté AB.
Solution :
Le triangle est rectangle en A, donc l’ hypoténuse est le côté BC ( le côté opposé à l’angle droit )
Donc, on applique le Théorème de Pythagore :
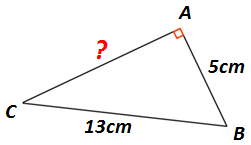
Exercice 3 : Calcul de la longueur de l’un des 2 côtés
Le triangle est rectangle en A ( AB = 5cm, BC = 13cm et AC = ? ).
Question : Calculer la longueur du côté AC.
Solution :
Le triangle est rectangle en A, donc l’ hypoténuse est le côté BC.
Donc, on applique le Théorème de Pythagore :
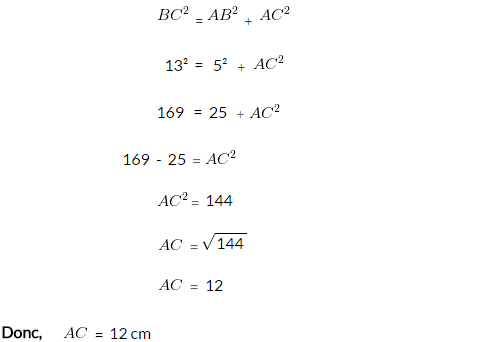
Autres Exercices Corrigés :
Les trois premiers exercices sont corrigés. Par contre, les trois derniers, vous n’ avez pas de correction et vous pouvez laisser vos réponses en bas en commentaire et nous ne manquerons pas de vous répondre ( écrivez toutes vos démonstrations détaillant comment vous avez trouvé les réponses ) :
Exercice 1 : Calculer une longueur dans un triangle rectangle
Pour chaque cas, tu calcules la longueur qui manque en appliquant la Formule de Pythagore :
| Le triangle ABC est rectangle en … | AB | BC | AC |
| A | 5.76 | … | 5.2 |
| B | … | 12.96 | 59.04 |
| C | 549 | 99 | … |
Corrigé :
| Le triangle ABC est rectangle en … | AB | BC | AC |
| A | 5.76 | 7.76 | 5.2 |
| B | 57.6 | 12.96 | 59.04 |
| C | 549 | 99 | 540 |
Explication :
Cas 1 : triangle ABC rectangle en A. Donc l’hypoténuse est le côté BC et on cherche à calculer le côté BC
BC² = AB² + AC²
BC² = 5.76² + 5.2²
BC² = 33.1776 + 27.04
BC² = 60.2176
BC = 7.76 ( 7.76² = 60.2176 )
Cas 2 : triangle ABC rectangle en B. Donc l’hypoténuse est le côté AC et on cherche à calculer AB
AC² = AB² + BC²
AB² = AC² – BC²
AB² = 59.04² – 12.96²
AB² = 3485.7216 – 167.9616
AB² = 3317.76
AB = 57.6 ( 57.6² = 3317.76 )
Cas 3 : triangle ABC rectangle en C. Donc l’hypoténuse est le côté AB et on cherche à calculer AC
AB² = AC² + BC²
AC² = AB² – BC²
AC² = 549² – 99²
AC² = 301401 – 9801
AC² = 291600
AC = 540 ( 540² = 291600 )
Exercice 2 : Calcul de la longueur de l’ hypoténuse
Prenons un carrée DEFG de 6 cm de côté. Calculer la longueur des diagonales de ce carrée. ( le résultat doit être arrondi au centième de centimètre ).
Corrigé :
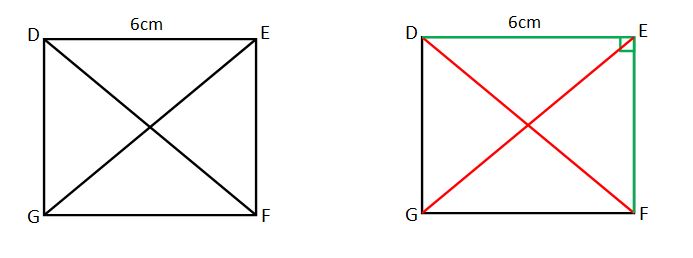
On a la longueur de chaque côté du triangle est 6cm.
Pour calculer la longueur de la diagonale, on prend le triangle DEF rectangle en E et on applique le Théorème de Pythagore :
DF² = DE² + EF²
DF² = 6² + 6²
DF² = 36 + 36
DF² = 72
DF ≈ 8.49 ( 8.49² ≈ 72 )
Donc, la mesure de la diagonale est 8.49 cm ( arrondi aux centièmes )
Exercice 3 : Longueur d’un côté différent de l’ Hypoténuse
Prenons le triangle ABC rectangle en A
On sait que BC = 17,1cm et CA = 15,1cm
Sans construire le triangle, calcule AB ( on donne le résultat arrondi au dixième près )
Corrigé :
Le triangle ABC est rectangle en A. Donc, l’hypoténuse est le côté BC
On applique le Théorème de Pythagore sur le le triangle ABC :
BC² = AB² + AC²
(17,1)² = AB² + (15.1)²
AB² = (17,1)² – (15.1)²
AB² = 292.41 – 228.01
AB² = 64,4
AB ≈ 8
Donc, AB = 8 cm ( Arrondi au dixième )
Exercices à Faire: Calculer une Longueur dans un Triangle Rectangle
Dans les trois exercice, il s’ agit de l’ application du Théorème de Pythagore pour calculer une longueur.
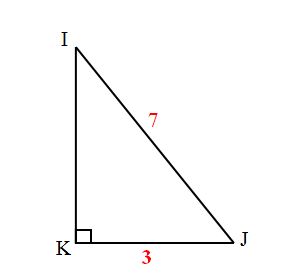
Exercice 1 : Longueur de l’ Hypoténuse
Combien mesure la longueur IK ? ( le résultat doit être arrondi au centièmes )
Exercice 2 : Longueur de l’ Hypoténuse
Calcule la longueur de la diagonale d’un carré de côté 12 centimètres ( le résultat est arrondi à 0,01 centimètre près )
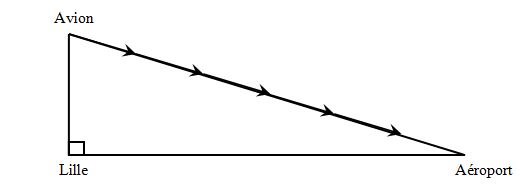
Exercice 3 : Longueur de l’ un des côtés de l’ angle droit
Supposant qu’ un avion vole au dessus de Lille et il doit atterrir dans un aéroport situé à 18 km de la ville.
En descendant, il parcourt 20 km.
Au dessus de Lille, à quelle altitude volait-il ?
Autres liens utiles :
Si ce n’est pas encore clair pour toi Comment calculer une longueur dans un triangle rectangle en appliquant la Formule de Pythagore, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête