Contenu
Définition d’ un Polygone Régulier
Un polygone régulier est un Polygone à la fois équilatéral (tous ses côtés ont la même longueur) et équiangle (tous ses angles ont la même mesure).
Origine du mot Polygone : le mot Polygone vient du grec polus qui veut dire « nombreux » et gonia qui signifie « angle ». Pour nommer les Polygones, on utilise un préfixe grec pour la partie numérique du nom suivi de la terminaison gone.
Par exemple, un polygone à six côtés est appelé un Hexagone et celui à neuf côtés est appelé un Enneagone.
Dans ce cours, nous allons voir la nomenclature des différents type de Polygones réguliers en fonction du nombre de côtés qui les constituent.
Polygone Régulier : Les figures les plus utilisées
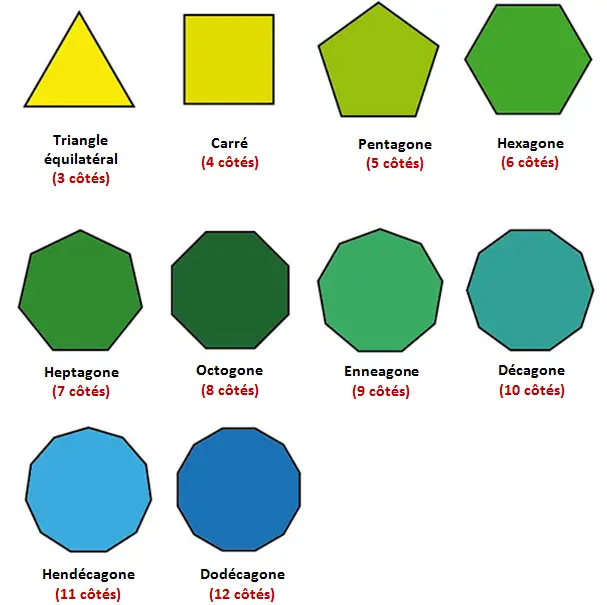
Ci-dessous, tu as les Polygones Réguliers les plus utilisés en géométrie et leurs noms dépendent du nombre total des côtés :
Polygone Régulier : Mesure des Angles au Centre
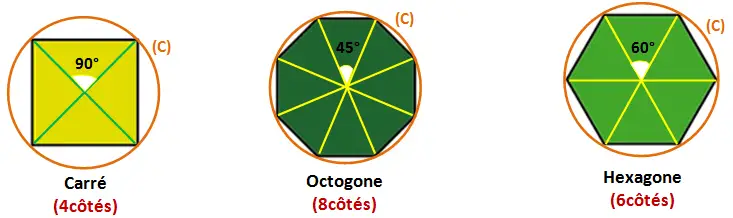
La somme des angles au centre d’ un Polygone quelconque est 360°.
- Triangle équilatéral : figure à 3 côtés donc il a 3 angles au centre. La mesure de chaque angle est 360° / 3 = 120°
- Carrée : figure à 4 côtés donc il a 4 angles au centre. La mesure de chaque angle est 360° / 4 = 90°
- Pentagone : figure à 5 côtés donc il a 5 angles au centre. La mesure de chaque angle est 360° / 5 = 72°
- Hexagone : figure à 6 côtés donc il a 6 angles au centre. La mesure de chaque angle est 360° / 6 = 60°
- Octogone : figure à 8 côtés donc il a 8 angles au centre. La mesure de chaque angle est 360° / 8 = 45°
- Dodécagone : figure à 12 côtés donc il a 12 angles au centre. La mesure de chaque angle est 360° / 12 = 30°
Et c’est pareil pour les autres Polygones Réguliers qui sont pas cités…
Autres liens utiles :
- Angle Inscrit et angle au Centre
- Formules d’Aires et de Volumes
- Agrandissement ou réduction de rapport k ( k > 0 ou k < 0 )
- Théorème de Pythagore ( Introduction )
- Calculer la longueur d’un côté dans un triangle rectangle ?
- Réciproque du théorème de pythagore ( Exercice d’ Application )
- Contraposée du théorème de pythagore ( Exercice d’ Application )
Si ce n’est pas encore clair sur les Polygones Réguliers , n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
